In this post, I will try to describe my knowledge about SNARK. By the time I’m writing this post, ZK Hack Discord is running ZK Whiteboard Study Group and they are discussing about SNARK, so maybe I’m lucky :D

Resources

ZK Whiteboard Sessions - Module One: What is a SNARK? by Dan Boneh

zk-SNARKs: A Gentle Introduction by Anca Nitulescu

Detail

What is a SNARK ?

In the class of non-interactive proofs, a particularly interesting concept for proving integrity of results for large computations is that of SNARK, i.e., succinct non-interactive argument of knowledge. By this term, we denote a proof system which is:

• Succinct: the size of the proof is very small compared to the size of the statement or the witness, i.e., the size of the computation itself.

• Non-interactive: it does not require rounds of interaction between the prover and the verifier.

• Argument: we consider it secure only for provers that have bounded computational resources, which means that provers with enough computational power can convince the verifier of a wrong statement.

• Knowledge-sound: it is not possible for the prover to construct a proof without knowing a certain so-called witness for the statement; formally, for any prover able to produce a valid proof, there is an extractor capable of extracting a witness (”the knowledge”) for the statement.

Examples:

• I know an $m$ such that $SHA256(m) = 0$

• I know $x$ such that $g^x = h \mod p$

SNARK systems can be further equipped with a zero-knowledge property that enables the proof to be done without revealing anything about the intermediate steps (the witness). We will call these schemes zk-SNARKs.

zk-SNARK is really fit with blockchain, so we have lots of applications

Mathematical Background

Arithmetic Circuits

Let $\mathbb{F}_p$ is a finite field with $p > 2$, then we can define Arithmetic Circuits as:

• A directed acyclic graph (DAG) where internal nodes are labeled $+, -$ or $*$, with input $x_i \in \mathbb{F}_p$ and $1$.

• An $n$-variate polynomial with an evaluation recipe

• A map $C: F^n \to F$, with $|C|$ = number of gate

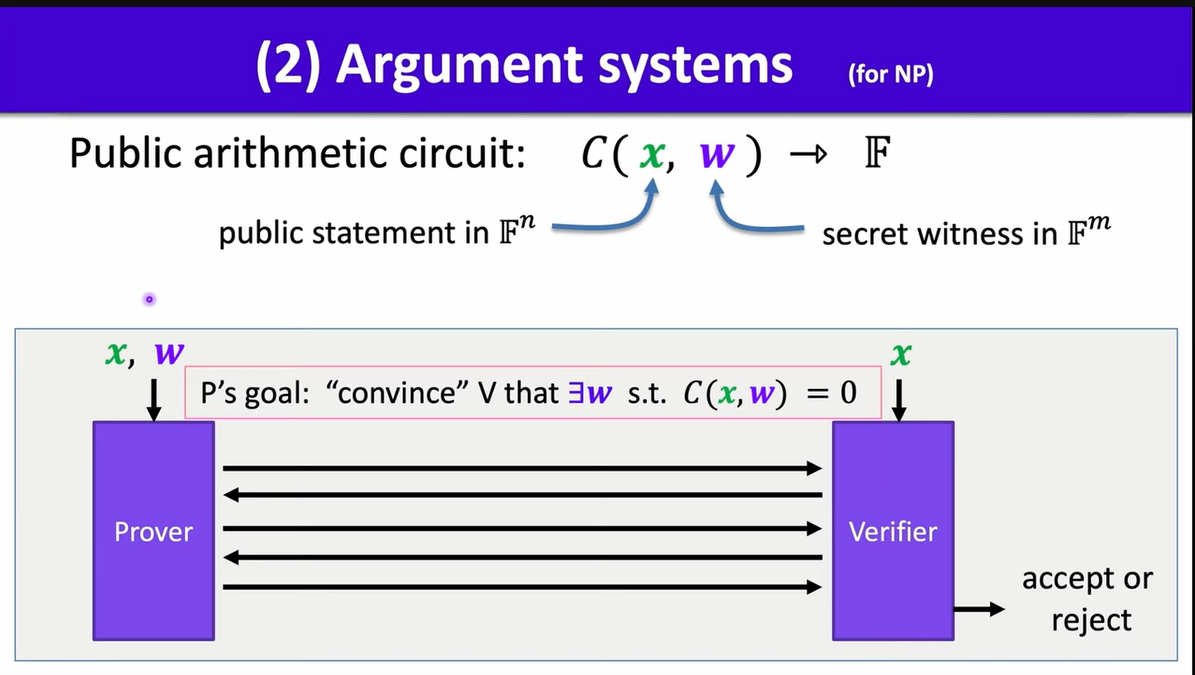
Argument Systems

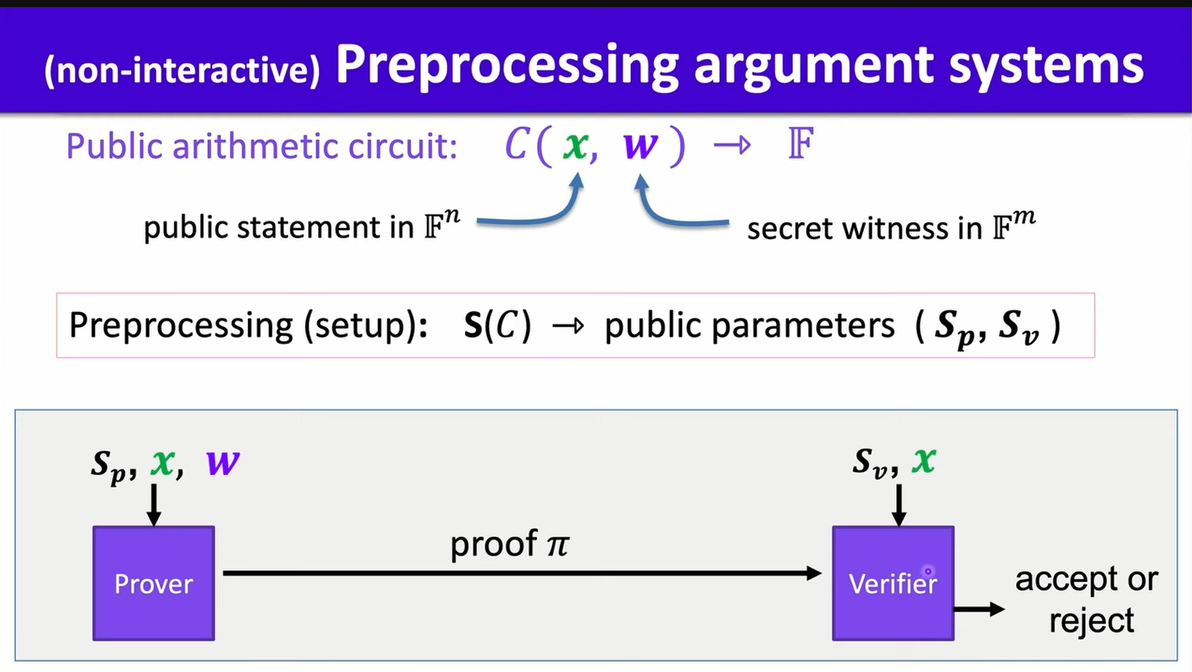
A preprocessing argument system is made up by three algorithms: Setting Algorithm, Prove Algorithm and Verify Algorithm (S, P, V):

• $S(C) \to$ public parameter $(S_p, S_v)$ for prover and verifier

• $P(S_p, x, w) \to$ proof $\pi$

• $V(S_v, x, \pi) \to$ accept or reject

An argument system requires:

• Complete: $\forall x, w: C(x, w) = 0 \to Pr[V(s_v, x, P(S_p, x, w)) = accept] = 1$

• Soundness: If $V$ accepts, then $P$ “knows” $x$ such that $C(x, w) = 0$, and if $P$ doesn’t know $w$, then $Pr[V(s_v, x, P(S_p, x, w)) = accept] = negl$

• Zero Knowledge:(Optional) $(C, S_p, S_v, x, \pi)$ reveal nothing about $w$

SNARK: Succinct Non-interactive ARgument of Knowledge

A succinct preprocessing argument system is made up by three algorithms: Setting Algorithm, Prove Algorithm and Verify Algorithm (S, P, V):

• $S(C) \to$ public parameter $(S_p, S_v)$ for prover and verifier

• $P(S_p, x, w) \to$ short proof $\pi$; $|\pi| = O(log(|C|), \lambda)$

• $V(S_v, x, \pi) \to$ accept or reject, fast to verify; $time(V) = O(|x|, log(|C|), \lambda)$

Types of preprocessing setup