Hack The Boo 2023
Table of Contents
Hack The Boo 2023
Last week, I played Hack The Boo with my team @phis1Ng__. I solved all crypto challenges include 3 in Hack The Boo - Practice, and 2 in Hack The Boo - Competition. All challenges are not too hard but not too easy, so I decided to write a writeup for all of them.
Hack The Boo - Practice
1. Hexoding64
chall.py
from secret import FLAG
HEX_CHARS = '0123456789abcdef'
B64_CHARS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
def to_hex(data):
data = int.from_bytes(data, 'big')
encoded = ''
while data:
i = data % 16
encoded = HEX_CHARS[i] + encoded
data >>= 4
return '0' * (len(encoded) % 2) + encoded
def to_base64(data):
padding_length = 0
if len(data) % 3 != 0:
padding_length = (len(data) + 3 - len(data) % 3) - len(data)
data += b'\x00' * padding_length
bits = ''.join([bin(c)[2:].zfill(8) for c in data])
blocks = [bits[i:i+6] for i in range(0, len(bits), 6)]
encoded = ''
for block in blocks:
encoded += B64_CHARS[int(block, 2)]
return encoded[:-padding_length] + '=' * padding_length
def main():
first_half = FLAG[:len(FLAG)//2]
second_half = FLAG[len(FLAG)//2:]
hex_encoded = to_hex(first_half)
base64_encoded = to_base64(second_half)
with open('output.txt', 'w') as f:
f.write(f'{hex_encoded}\n{base64_encoded}')
main()
output.txt
4854427b6b6e3077316e675f6830775f74305f3164336e743166795f336e633064316e675f736368336d33735f31735f6372756331346c5f6630725f615f
Y3J5cHQwZ3I0cGgzcl9fXzRsczBfZDBfbjB0X2MwbmZ1czNfZW5jMGQxbmdfdzF0aF9lbmNyeXA1MTBuIX0=
The flag is splitted into 2 parts, part 1 is converted to hex and part 2 is encoded by using base64 encode, so we just need to convert each part to bytes
flag: HTB{kn0w1ng_h0w_t0_1d3nt1fy_3nc0d1ng_sch3m3s_1s_cruc14l_f0r_a_crypt0gr4ph3r___4ls0_d0_n0t_c0nfus3_enc0d1ng_w1th_encryp510n!}
2. spg
chall.py
from hashlib import sha256
import string, random
from secret import MASTER_KEY, FLAG
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from base64 import b64encode
ALPHABET = string.ascii_letters + string.digits + '~!@#$%^&*'
def generate_password():
master_key = int.from_bytes(MASTER_KEY, 'little')
password = ''
while master_key:
bit = master_key & 1
if bit:
password += random.choice(ALPHABET[:len(ALPHABET)//2])
else:
password += random.choice(ALPHABET[len(ALPHABET)//2:])
master_key >>= 1
return password
def main():
password = generate_password()
encryption_key = sha256(MASTER_KEY).digest()
cipher = AES.new(encryption_key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(FLAG, 16))
with open('output.txt', 'w') as f:
f.write(f'Your Password : {password}\nEncrypted Flag : {b64encode(ciphertext).decode()}')
main()
output.txt
Your Password : gBv#3%DXMV*7oCN2M71Zfe0QY^dS3ji7DgHxx2bNRCSoRPlVRRX*bwLO5eM&0AIOa&#$@u
Encrypted Flag : tnP+MdNjHF1aMJVV/ciAYqQutsU8LyxVkJtVEf0J0T5j8Eu68AxcsKwd0NjY9CE+Be9e9FwSVF2xbK1GP53WSAaJuQaX/NC02D+v7S/yizQ=
Looking at generate_password() function, we know that the password is generate based on each bit of MASTER_KEY: if the bit is 1, we will have a character in ALPHABET[:len(ALPHABET)//2], otherwise we will have a character in ALPHABET[len(ALPHABET)//2:]. So we can reverse the password to see with bit is 1/0 and recover MASTER_KEY
solve.py
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from base64 import b64encode, b64decode
from hashlib import sha256
import string, random
pwd = "gBv#3%DXMV*7oCN2M71Zfe0QY^dS3ji7DgHxx2bNRCSoRPlVRRX*bwLO5eM&0AIOa&#$@u"
enc = b"tnP+MdNjHF1aMJVV/ciAYqQutsU8LyxVkJtVEf0J0T5j8Eu68AxcsKwd0NjY9CE+Be9e9FwSVF2xbK1GP53WSAaJuQaX/NC02D+v7S/yizQ="
ALPHABET = string.ascii_letters + string.digits + '~!@#$%^&*'
master_key_bin = ''
for c in pwd:
if c in ALPHABET[:len(ALPHABET)//2]:
master_key_bin = '1' + master_key_bin
else:
master_key_bin = '0' + master_key_bin
master_key = int(master_key_bin, 2).to_bytes(len(pwd), 'little').strip(b'\x00')
encryption_key = sha256(master_key).digest()
cipher = AES.new(encryption_key, AES.MODE_ECB)
flag = cipher.decrypt(b64decode(enc))
print(unpad(flag, 16).decode())
flag: HTB{00ps___n0t_th4t_h4rd_t0_r3c0v3r_th3_m4st3r_k3y_0f_my_p4ssw0rd_g3n3r4t0r}
3. yesnce
chall.py
from Crypto.Util import Counter
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
import os
with open('messages.txt') as f:
MSG = eval(f.read())
class AdvancedEncryption:
def __init__(self, block_size):
self.KEYS = self.generate_encryption_keys()
self.CTRs = [Counter.new(block_size, initial_value=i) for i in range(len(MSG))]
def generate_encryption_keys(self):
keys = [[b'\x00'] * 16] * len(MSG)
for i in range(len(keys)):
for j in range(16):
keys[i][j] = os.urandom(1)
return keys
def encrypt(self, i, msg):
key = b''.join(self.KEYS[i])
ctr = self.CTRs[i]
cipher = AES.new(key, AES.MODE_CTR, counter=ctr)
return cipher.encrypt(pad(msg.encode(), 16))
def main():
AE = AdvancedEncryption(128)
with open('output.txt', 'w') as f:
for i in range(len(MSG)):
ct = AE.encrypt(i, MSG[i])
f.write(ct.hex() + '\n')
if __name__ == '__main__':
main()
messages.txt
[
'Hm, I have heard that AES-CTR is a secure encryption mode!',
'I think it is not possible to break it, right?',
'HTB{?????????????????????????????????????????????}',
'This is why I used it to encrypt my secret information above, hehe.',
]
output.txt
983641d252da35432cdd8aaa490b24bc5ac0583f5881adbe95c5b16d4309878a37c0d38d523f2b45390294e7ed7fe276a1ac966868a34e1284f6215389342b35
3394443645cf87dbaf9cd2506209809663818391442f37553047d1fde12df974b0a4922621ba0d5693be403dfb0d2f31
5ff5b1855a683504035184fbbd52e236a09ac86879ba10428de65d66d0065f412ed765fb2593aef817a6c59ed373ee8192ab659a30b06723ee9d363e00e2c7f7
81ad907568a7525696bf5e75c61258407fca36cd25dbe9c845f2cc95d555e9c1cbbb12b44ddb0a5f85e71859608aa68b271836560e3ecabde06ca9dddd35c9dd027436cf1facf536e9b7a51d5d09bbf5
A challenge using AES-CTR with many counters and keys. First time I see it, i feel a bit confused because it looks unbreakable, and I don’t have many knowledge about this mode. So how can I solve it?
1. Keys
def generate_encryption_keys(self):
keys = [[b'\x00'] * 16] * len(MSG)
for i in range(len(keys)):
for j in range(16):
keys[i][j] = os.urandom(1)
return keys
When read it in the first time, I think this function will generate different keys, but it’s not!
This line
keys = [[b'\x00'] * 16] * len(MSG)
will make many keys at the same address, so when we change an element at index i in any key, we will change all the element at index i in all keys
To check it, you can use function id() in Python:
keys = [[b'\x00'] * 16] * len(MSG)
for key in keys:
print(id(key))
And you will see this
140544276991168
140544276991168
140544276991168
140544276991168
To fix this problem, you can make in this way:
keys = []
for _ in range(len(MSG)):
keys.append([b'\x00'] * 16)
Now, when use function id() at the same way below, you can see this problem is fixed!
139887490715264
139887490715328
139887490715776
139887492162176
2.AES - CTR
We will look at AES-CTR Mode
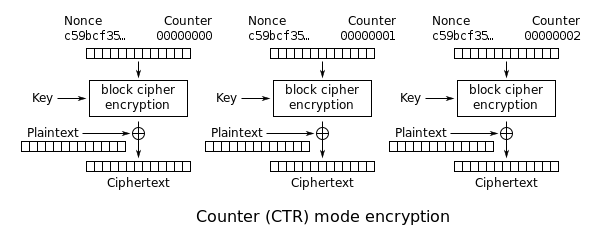
We see that the counter is increasing by 1, and luckily, counters in this challenge are generated by this way:
self.CTRs = [Counter.new(block_size, initial_value=i) for i in range(len(MSG))]
And here is counter block sequence
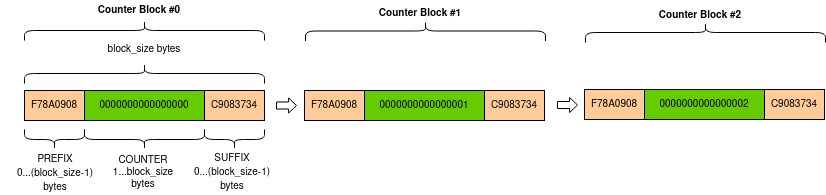
Look at how CTRs is generated again, we see that each counter doesn’t have prefix or suffix, so the counter block consist entirely of counter value
Another problem, where is the nonce ? From the documentation of PyCryptodome, a 8-byte nonce will be generated whenever the nonce parameter is not present.

So the nonce is reuse, and we will have all we need to do the attack: The known-plaintext keystream-reuse attack
Because the keystream is the same for all file, except it is left-shifted 16 bytes for each message, so to find the message, we using this:
$$C \oplus (K « 32B) = P \oplus (K « 32B) \oplus (K « 32B) = P$$
as well as the other message using their respective keystream shifts
solve.py
from Crypto.Util import Counter
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
from pwn import xor
with open('messages.txt') as f:
MSG = eval(f.read())
ENC = [bytes.fromhex(c) for c in ['983641d252da35432cdd8aaa490b24bc5ac0583f5881adbe95c5b16d4309878a37c0d38d523f2b45390294e7ed7fe276a1ac966868a34e1284f6215389342b35', '3394443645cf87dbaf9cd2506209809663818391442f37553047d1fde12df974b0a4922621ba0d5693be403dfb0d2f31', '5ff5b1855a683504035184fbbd52e236a09ac86879ba10428de65d66d0065f412ed765fb2593aef817a6c59ed373ee8192ab659a30b06723ee9d363e00e2c7f7', '81ad907568a7525696bf5e75c61258407fca36cd25dbe9c845f2cc95d555e9c1cbbb12b44ddb0a5f85e71859608aa68b271836560e3ecabde06ca9dddd35c9dd027436cf1facf536e9b7a51d5d09bbf5']]
msg1_keystream = xor(ENC[1], pad(MSG[1].encode(), 16))
msg2_keystream1 = msg1_keystream[16:][:len(ENC[2])]
#print(xor(ENC[2], msg2_keystream1))
msg3_keystream = xor(ENC[3], pad(MSG[3].encode(), 16))
msg2_keystream2 = msg3_keystream[16:48]
print(unpad(xor(ENC[2][:32], msg2_keystream1) + xor(ENC[2][32:], msg2_keystream2), 16).decode())
flag: HTB{m4k3_sur3_y0u_1n1t14l1z3_4rr4ys_th3_r1ght_w4y}
Hack The Boo - Competition
1. symbols
chall.py
from secret import FLAG
from random import randint
p = 307163712384204009961137975465657319439
g = 1337
def encrypt(m):
bits = bin(m)[2:]
encrypted = []
for b in bits:
r = (randint(2, p) << 1) + int(b)
encrypted.append(pow(g, r, p))
return encrypted
def main():
flag = int.from_bytes(FLAG, 'big')
encrypted_flag = encrypt(flag)
with open('output.txt', 'w') as f:
f.write(str(encrypted_flag))
if __name__ == '__main__':
main()
output.txt
[236195756868517656723513582436861606906, 57834783484301373179714799552205481954, 267720308275932715147205375538382826955, 149092033205073279855511853881589809010, 58424761794072998702558565907923210061, 1474110831190262608109442199483811396, 163053413501521220432813224719322520343, 119823699155184027043969102805062191441, 159571890149858495555307399445325012284, 195717201450729986508861286257046392334, 114431778290475226872809734457174018792, 218162028253871849172261202156083591640, 109672631939007910803691571069172981811, 193433512850089598853923720218322897666, 203707553307882002060636523391132788830, 165178305100165779779082572019143752076, 168112790210921765812613688558600521933, 259295183477837074170544386397411962537, 72159425377499728967395838521170265678, 61257639550003930626655558573570375667, 53912044472574402035294330397655014508, 226759619237657768020688997684351249522, 207669219042336576373060372576522188926, 62218709641327619861361701519347901903, 221930182162000427234878462314905615934, 103905100137359639759778538644836993114, 122085512968076140186478249097034194620, 79790132810657519260425461575563651014, 105720237588559999443513176173321207812, 4141874793962506085501192334821873588, 258260700143946447861527599261604556990, 304836041323039503483423294942352823225, 74711472409612511216985339518022873265, 281293548316789520771629451289333366059, 33315385586376261091605566022845019165, 195031151608254832747861469332299766779, 8874453320499641503217809067221226651, 218372886049824560689090550490862269745, 49443672021619856243541967231484922934, 3797928589787299936105903884032628983, 233232957701005845474826605663076782322, 225717577262646644076173305131793012952, 217674854438450569168330544830834890239, 112632127397310466151290839212576069250, 297054153782140787762508061528667326334, 200864923363562552986304896619830418825, 207814447965726601601459303467914840668, 183268898499264583001015073048851916267, 302323867260523032831652951482239931870, 121811779197657018566930567987706650145, 197939160714477105354408139112513818588, 242467408311754766994790469368889328898, 125047863006239061494525332911274359824, 256055239004494720079913801004332470083, 125481538676534939361509260427893757231, 151961354577514699876702118550614978524, 139337233502703760972938620054847414082, 54273025797683328748801507686107401875, 20653194921403421700512039686521584608, 4016737468201962410736344683218936054, 89329187741361387359560746315142203118, 225406976281509920555422230168821297298, 191990134569339659970088329840165511825, 230851829782994261833309017999787924324, 116560901475560555203390303370847962630, 242922874400477413665861083227177676592, 158273966342641837379946400042003253821, 192463194708815919706398960822785854561, 88590986965981017167863091396039010259, 125699959791975424231829606670777297509, 4674062135079405678161986278960978859, 295915697039920278742246054056568248046, 153777500463526326680976578455362797868, 293641984445847968623799820749440556400, 278260155507943247430558495672029343269, 116970199964828316399106934265923277177, 141314664087726853403505171598611919153, 249880828871252544637608762004255492665, 75397135144827510989108863721550837615, 25838141974541593100207855375396418337, 26744542605064423411838425224569882883, 111479658873107426450034025232787393071, 122711549557000570999859254230225985996, 234452168130798426103090678301960430088, 83344563444820883307048423914760857323, 285842052907810469311410015384329848393, 191261144309106677852390682025226532253, 78694100597213810147271333579864536178, 173848085329452212926926348067495134194, 64022993630438250686170301246585182721, 63009085631787857429160386034458198051, 32480634537935362268355670906886932080, 15767933517959013175137111051917516119, 71366103925656507820659219493116240126, 101691033666002415795570133186208824977, 69077658268707695484939357549270516417, 198008703086408244773830406047222547556, 237395086066778758585182789083839256019, 205904022862678237509786919700364500959, 93211126636702829233154574509713589989, 256772439038083190309486076111014772656, 117571035407272577532112292917924278022, 136565134972912087872852453761091589160, 302903980502928774842775159472377670659, 298208918278247203432422660467294890950, 247097638235639481178843100500741237318, 134638530165023910128750529207711830960, 296279440176443131848519174817772138477, 165607260838070337290216988963065657083, 54911438888497322338109298177844240543, 168091545668922619001185882538771831439, 12215198757054277945398872885469039147, 122780515235756935579877715051906605546, 227020386677629300158182259879513885762, 74128308616899714992851545962325008402, 202563904115494462045595239113178641323, 149831878127553695987542192078256701710, 238152846378867475824845759737563349039, 278975537557617527678850286807410984472, 62613765016341084522786354050558351860, 296416498974660277931027536134376948346, 298156951068506317844513484521568851490, 184857979739230402610346646714463615285, 18215115330156213991963479735615174612, 246575730483301894676542218420556342453, 288099039376805825533003504758225360291, 191480423471330209234209054269123597554, 71084901912387674608479851321519928803, 45025071362222616113441090389072097071, 47620844975568098051343557505789982861, 298988967095500526924406670118972931260, 274276110781743436003951153676720478208, 130051356372257282201920118270791087716, 168916731432425112528932729279316481951, 225007381772166558729133871780815889731, 19725433433059362390974491854784109938, 255915832194239778048105829254853414726, 6644537965927963748198410436363467288, 163097611704424430946284387974035660349, 48389408225757261676459402198619415601, 61532562092874334447628732019654365804, 257755096243341069093312281254996172530, 247936228891023955947779262224689661380, 37224790653696805486661551965348336941, 89025744901662857405455718528011117409, 60327330352788361126613658737898278840, 74344193034206774178892060428966116376, 99784993351916151851963129920650514530, 152791116215170114868237524767153153802, 121338741590551548864430726541831702247, 30438637110699532867010569930825901434, 221617393582282874954397442060287758793, 14335452200619389704697216360554150486, 266995951927721576787062579738384941652, 281343126394302164903102667378494617352, 16739553438865022310592036238508977330, 253605084816117830134213395574634463053, 17384228471503215307237391182318780430, 216055509119502048997741680911789269797, 184507338305919388856283781529498633535, 51389227945438052497410296595640795704, 182500594593682723835476489937944895338, 85313866949219500557954565524206618756, 255933139989091469559877467758030327253, 204221676677881668915398948904684105139, 201886330940557766757109782145016304770, 63727781773389659124509558143155049119, 164577570238479135052249983309370554778, 115887181697954014087831883275734193081, 257076910446287373230455041235610692953, 208246011947463918290284535660262795719, 307105846442992112962542896686899770051, 121976208912564964708698710006201593571, 163461558927216486634752210087176402455, 290519313398890946595778740210070336240, 39203578724350145282500607866944398967, 36523367157502206102320447880131433844, 239158505405518099010344289063727310109, 243068194421293287816921280815087141790, 115947026056914530480508458123557660006, 80361565875364590423052169473490309212, 228007972455330275193466018159013433399, 134878085638954763841868802087259023596, 126591485019910341476262982620391507528, 118018557764442719612409042878868887697, 175147784961440782032159796888417850042, 96604741734837402795929961836428550283, 115232088396576913784926728654494159155, 106844211943253380430858231501962723551, 63724090034639938418527698826192190939, 183267820914390636517030558110527813450, 139481782792347806645625197109286281120, 121824936515060660633139132885887499509, 8711110773158345810088636822685682128, 124698954991793872069705307233086457583, 164245012941658709485225086084374233148, 157399147837313309316589350353131069565, 12780681122629277316433056617016959595, 209378556853742644514050481232965095819, 25507075573308575203960763012617360890, 286351492453862354434326436861658392289, 36558436246048335181380188335192579745, 248219506497737852157148440403355874294, 167052573917454348660976630103224461763, 287742508661132192679080142777326943078, 214739677620109734459757547397409471726, 43519490587480378265122136825365148297, 264055517464798835137048684481896521027, 184326284522391984806573933461104011431, 44312092754397009855216164718045393529, 264119759594177981502747517417334293096, 231414584115935009145680519630602573691, 172539931164133296022607545277616306205, 250790905503673347740179537105576289757, 100585924827282275356136738210910608317, 291175888026300278788944252184398225125, 123696827599086998573981831183879350990, 2714736006483713948364807805417050020, 88733050593640685036147902835072291514, 245949917889787416890372591178866160759, 149705592266286677351645289140172981365, 230528475189017384850586421963905015996, 3099453341705819769647982816039023583, 205601700086886362121938960970307872784, 3198233509586496931157640450973851894, 303359660981657618955290356323663714981, 53080026997598326189063046677156042263, 12714480048192740511666984652343564346, 212888039401798018228261148638975121006, 248923232574268778482155483906179481919, 9200775760650755894188275376278954956, 42907096522449491990857339940972309324, 235480951988870887019575287286880601264, 293133213198426097957882572248927314596, 196832033324586505625417235977142479515, 122705993887041956554246104507107895409, 108930112678453882813097048888517740026, 228759717969465092631433676028477838418, 304220599780001881438247991395753464783, 247699159660177899954351863795037449427, 275954641831049011183199826362274348150, 62235924022379692600390452595282611159, 153964122875902668860592613490799863065, 7344457580103426721894059292348121307, 138129528902400549074393680724652685460, 159315655303173638975535262737876992270, 69693847123803815575660789144207379006, 298099532115413882220744068548490459339, 205862690430932330159215811046997635726, 96317282826485586400864298654644481887, 23937935386088941151058501310619472716, 145947278542188427028262512698338375558, 267452453646135270741219728053170391028, 288777494479956244519361188932901789376, 189007828638707729316967591964525836716, 234999483132413547429813569972270710947, 96818691916198330670623725451046553945, 215934053902817601850452667648128844911, 274463243428737114462024956225263986236, 31511281927617313382900876235136549967, 262766372668962845198793862636348799289, 14300182111226453525099656894243318562, 157479395673257614656221512912298657316, 89722147804475163613425581258122084223, 10537630147990422486988159119205807485, 43905505729292249543997847489728001109, 249022795202149221294807001666358809127, 280991707374757320685631136221711018424, 9334192016863140524107799111418272158, 102542812213063790129052110380749499250, 33375019399194492081238475705898606539, 230108062771962518992670788864093732153, 38971363207231658575341873575053872898, 252735959260023414878941933950360223528, 99437350362178867106495056411160140892, 261273561464335304223117862121010299160, 51893977578780771348561944270086680742, 134947265937359026966137347794039001160, 261879558177400947692509741360573074954]
Reading encrypt() function, we know that the message was encrypted bit-by-bit. We will see that if encrypted[i] is a quadratic residue mod p, the bit will be 0, otherwise it is 1 and we can use this way to recover flag
solve.py
from Crypto.Util.number import *
with open("output.txt", "r") as f:
encrypted_flag = eval(f.read())
p = 307163712384204009961137975465657319439
g = 1337
flag = ''
def check(n:int):
return pow(n, (p-1)//2, p)
for enc in encrypted_flag:
if check(enc) == 1:
flag = '0' + flag
else:
flag = '1' + flag
print(long_to_bytes(int(flag[::-1], 2)))
flag: HTB{l3g3ndr3_symb0l_1s_0v3rp0w3r3d}
2. leak
chall.py
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
from sympy import nextprime
import math
from secret import FLAG
MAX = 0x100
def factors():
return [getPrime(int(math.log2(MAX))) for i in range(int(math.log2(MAX)))]
class RSA:
def __init__(self):
p, q, self.leak = self.craft_primes()
self.n = p * q
self.e = 0x10001
def craft_primes(self):
numb = 1
count, p, q = 0, 0, 0
for i in factors():
count += 1
numb *= math.prod(range(1, i))
if count == 4:
p = nextprime(numb)
if count == 8:
q = nextprime(numb//p)
return p, q, numb
def encrypt(self, m):
return pow(m, self.e, self.n)
def main():
rsa = RSA()
ct = rsa.encrypt(bytes_to_long(FLAG))
with open('output.txt', 'w') as f:
f.write(f'{hex(rsa.leak)[2:]}\n{hex(rsa.e)[2:]}\n{hex(ct)[2:]}')
if __name__ == "__main__":
main()
output.txt
74a379eaa82fda90065ae3fef17fb5e5823f0aa0db7bdf7af2acfc18eacad62caa1d860234ddcf8ce8bd54704d96035c01605687bfcb9f08b114eb6326b25b60dccbd0b5b04dbc1c83d2460948ad6380555065f87183b0973d4c1f567c34d052d7e17acbacb47cb44049e25b4c34d00e6185e5fb6ea85411a08cf4172a675aff69ceb1e0d9a60f45c16de9cc0977a663310da92a1c217df4c47d26ea763754eff894d8c7d8f268f1b1a686c076ad9bb433fe1b69633d8033498d53f13f4b5bd35a7955b2f82ea500fa0536d13f5bebc2b24b726e337048bbf1a46122cd39bae21536aafbedd1214133e541ce6f75f859a1163002d0fb0468b2f8c6e03a10e89e80047f80a3e4c39955a18de014d03c62dd33cfe828de54bfff32bb463cb16047ca1fb9ee0f9dbccd0ce174ec62c64e638e9146c3db0e625f5f9163fd0885f0c0c404978100f502252adcdac7c438f531368c561162466f59a67c232a802c4f5e55135c31051d13627d24a6ec99ce1eb5c422af27ea7aac2f17dbce5b2795f21794b095b41a66b9b310d39b88c6429e0bcb54ef79d1a4ab23ed91b89dd30a2d8b1e3e963729efd70fde2166a275619eafb85000a687cd22375b0bf0d3c333d122ef856789e99af39a85fb4eadbf8bf81914c50b4151c23d5fb4ed0f23fe1ae1880ca3b467d66b7e60ef5306e1950f2bc7f885436354be09dd6b727746815e42c9b0703a12ca206647de0deb676b503b437716243eb7dfa4f9fe8b7e1cba8e1f0c97509c8ba32fd3393d5ef59a35e69a760aaa0cfd9917d1b196dc4357ec018e3cb19e5df02e3a64b05dfe8c22d71941ef2918b93836ca120ad498cad5902550e50b2dc924182af9ad53224dc2ac80920041c5fe4e692ff3fbc074bbc4584a87ed4e94a111ec046230165e7b5f6572b1a4e99d3c00b31bddbb1022a226d528e879813328886032c5566d1bd11b71236a0648393dceb95eda1e570c53af409a3603af1ef3368d4ac9313a82b9e117c5dbb1464b94f65ccbedcc727e19496de733453b1bbf4185ee1eb7f91d9ef7e9be4c5471acc6e99d2000280238ddee35874f9b5a75ec09666444aea51fda2261c3796072f8164cc7002c8c514282d4a685e2b79d8b4de61f5dea2e532fa66abde5b76ce8c9bef17d65d440a882328d7cfc487ddf7002730f111b779ee5b288b29feb31c0049d5ef0ea9164a7e96a973707a540e3fc1b43af2430fe5108289f0655b188eeb6ead6d6ba2943942817c573d04e6283b055efb1abf7681825b057a3c302c357760edabca6242024a29e2b77a0309e77000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
10001
56e32d922377ee6598e05e04fc4550283df774cb81ab9344751de5537f781c772871d1e391861e57788ec19c3f007c9d1f6b6dbc0e742e2387d8679742ba6bb8e16cb56dfcbc53768a1ede8c5c3b4aed1fcecfbaa690177ca80d347c727ca727c63dcd83aa31af1e7c6eb89192fcc24b53449c76e62a26360527c0b82006aa8f8f4d3b7b3c4a075fc859d3ee2a11c80997c13474b5fed58ac06e66d5fa2a401d20b58a8b5742f43cd7adb4c582e26065a38a6566525cc80b4467afbeb68dc68eddfe8f6dba37c14a7e437766d0915b0e2f4917e556fe1a2a1078ceda12fbd2251501e3ea3a47a68f426958fec98027d89c2dc73ced7a8b883ce19ed5d7c40daefe233c1b916c897b9a1df90eab1bbad8995b73a0256e3ec502cb2f07f7ee8bd83c320c3b2a89d6b040004442f831a632f81c44bf0e851a42d061eb4c767dd98787f560afadacb65e5f3af1587b52875ade78103cf29112ce1c9e8c75db4fc490fd61d59a64d1bdd4a54dc949e4a72e1fb33d730f3cc791dfc329de6051c013b8f404d03083ee4f4e9e55993be3890f9866634b4ef1aec298ebdb9b80ffa509dd5ade0730447fd06d6f3cedece57f45a5aeb87014de2b22179b84a3fa131f8e214dc690db9bb099ce60075e4298846f9c4e3b57643af401e290780630dd3c4aec7884d801ddd8367c6844182387a589a0b17a53aa63a8d863bb44aa397c1eaad36a083ce2de0ec4cd1fcce26a38acae00d9515fd2f8475695d6496866cb3ae92f36d4a932b73ffe15f1dfeb8b7314336a4e2dd97caa0c30cb24e592e92c89651e8299022990cacbd917c850cdec525fd6517cb9f470c434b8cd416aeb00c994e7df962f7a020b052496dabfdc6876efdbb7696c02000e73b2c668aae41356840a45702335ef76e3bab4d9287fa743c22e945f9c3c7e9ed76449cd2f1d47bab3633d7c2bbbbc21c6bab2736df6400bfe84e194e030904d31bcf36123ba5d48c5c42e3b5a01a9d1ae959a074786f4b00753d3533b7621abc59dd4d3ef5222c596308b8c34dcef8fa48e0cc7447f5cab84d504495334dc7f75048257ff1d9a64d54d3f1be6e38ee138b5534585634fdcf9f3c0b7a1f6d9ce6102b6de74b09c6cd3e51ea0aef2cdd71088da294d776cae7d9f1574b843a81d99092a8a286d26f8bf58b39aa40fbbb4bcc96374936a49215e40e6155e877beb444990461c00fb13219fe800b3c77b678708c042de35769880e623f934c2d1b9626f407f3f8f53284bed18e4833210f1216d7373e5a82501e51b8bb3611e09fc9c1aec7190650256e83178adf454a5e1061be1aa16f21d08e443f603b89e6115eaddf19dbf859159629b433291cce0e2a532b5c7a68068d96c1cd8a889527f58c11be0427090412933a1bdd595b3a6e81e884401f295a84af097afab4bc9ea1d07c458e62c5a102bd6a07cbf92e1a105e36464f6b7d6112e7d736c64b705e7725d16e85fd5e13311bfb94198e64b2526fc423cf7ee109a726cccd93bd81739aeaef052557db081d8ed693ef1c1784e237494973d74ab7e04e53641a6
In this challenge, we need to recover factors and its sorting order
We will see that numb is generated by product of factorial of each 8-bits prime minus 1, so numb will have special divisor, which is the biggest prime which is smaller than factor[i]. So our algorithm to recover factors is:
- Generate an array which have all 8-bits prime numbers, denoted it by
A - Finding smallest number in
Awhich is not a divisor ofnumb, denoted it byk, it will be an element infactors - Divide
numbbymath.prod(range(1, k)), by this way,numbwill decrease and we will get an element infactors - If
numb == 1, returnfactors, otherwise back to step 2
After found all divisors, we just need to bruteforce all cases to find correct p and q. And after that, everything is trivial!
solve.py
#!/usr/bin/python3
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime, sieve_base
import math
from tqdm import tqdm
from sympy import nextprime
MAX = 0x100
with open("output.txt", "r") as f:
data = f.readlines()
leak, e, ct = [int(c[:-1], 16) for c in data]
def v_p(n:int, p:int):
ans = 0
while n % p == 0:
ans += 1
n //= p
if n == 1:
break
return ans
use_primes = []
for prime in sieve_base:
if prime in range(2**7, 2**8 - 1):
use_primes.append(prime)
use_primes.append(257)
def check(num):
for prime in use_primes:
print(prime, v_p(num, prime))
#Find factor
factors = []
while leak != 1:
for prime in use_primes:
if v_p(leak, prime) == 0:
factors.append(prime)
leak //= math.prod(range(1, prime))
break
factor_factorial = [math.prod(range(1, i)) for i in factors]
#Find p
p = 2
def find_p_q(index:list):
numb1 = 1
numb2 = 1
for i in range(8):
numb2 *= factor_factorial[i]
if i in index:
numb1 *= factor_factorial[i]
p = nextprime(numb1)
q = nextprime(numb2//p)
return p, q
for i in range(8):
for j in range(i+1, 8):
for k in range(j+1, 8):
for l in range(k+1, 8):
print(i, j, k, l)
index = [i, j, k, l]
p, q = find_p_q(index)
phi = (p - 1)*(q - 1)
d = pow(e, -1, phi)
m = pow(ct, d, p * q)
flag = long_to_bytes(int(m))
if b'HTB' in flag:
print(flag.decode())
exit()
flag: HTB{numb3rz_ar3_l3ak1ng_fr0m_3v3rywh3r3}